سلام و خسته نباشید
یکی از روش های جالب برای محاسبه عدد پی الگوریتم Gauss-Legendre هست که در برنامه Super Pi از اون استفاده میشه.
اعداد اولیه الگوریتم:
برای مشاهده این لینک/عکس می بایست عضو شوید ! برای عضویت اینجا کلیک کنیدتابع بازگشتی الگوریتم:
برای مشاهده این لینک/عکس می بایست عضو شوید ! برای عضویت اینجا کلیک کنید
مقدار تقریبی عدد پی:
برای مشاهده این لینک/عکس می بایست عضو شوید ! برای عضویت اینجا کلیک کنید
یکی از امتیازات این الگوریتم اینه که با مقادیر پایین n میشه به دقت بالایی از عدد پی دست پیدا کرد. مثلاً با مقدار n = 3 تا چهارده رقم اعشار پی (و شاید هم بیش تر) صحیح به دست اومد.
این الگوریتم رو به زبان #C نوشتم. امیدوارم به کارتون بیاد:
تنها مشکل اینه که مقدار Double فقط تعداد محدودی از رقم های اعشار رو نشون میده. فکر کنم باید واسه این مشکل هم چاره ای اندیشید!! اگه نیاز به همکاری در این مورد هست شاید بتونم کمک کنم.برای مشاهده این لینک/عکس می بایست عضو شوید ! برای عضویت اینجا کلیک کنیدکد:using System; using System.Collections.Generic; using System.Linq; using System.Text; // By Ali TM namespace Pi { class Program { static void Main(string[] args) { int n = 3; Console.WriteLine(Math.Pow(an(n) + bn(n), 2) / (4 * tn(n))); Console.ReadKey(); } static double an(int n) { if (n == 0) return 1; return (an(n - 1) + bn(n - 1)) / 2; } static double bn(int n) { if (n == 0) return 1 / Math.Pow(2, 0.5); return Math.Pow(an(n - 1) * bn(n - 1), 0.5); } static double tn(int n) { if (n == 0) return 0.25; return tn(n - 1) - pn(n - 1) * Math.Pow(an(n - 1) - an(n), 2); } static double pn(int n) { if (n == 0) return 1; return 2 * pn(n - 1); } } }
شاد باشید
نمایش نتایج 1 تا 5 از 5 مجموع
Threaded View
-
28-07-13 03:01 #4

 عضو VIP شهرسختافزار
عضو VIP شهرسختافزار
- تاریخ عضویت
- Jan 2008
- موقعیت
- Isfahan
- ارسالها
- 6,285
- تشکر
- 2,094
- 6,911 تشکر در 3,255 ارسال
 پاسخ: کودا (cuda) چیست؟ و برنامه نویسی تحت کودا
پاسخ: کودا (cuda) چیست؟ و برنامه نویسی تحت کودا
-
اطلاعات موضوع
کاربران در حال مشاهده موضوع
1 کاربر در حال مشاهده این موضوع. (0 عضو و 1 میهمان)









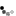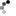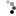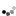
 پاسخ با نقل قول
پاسخ با نقل قول
Bookmarks